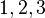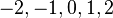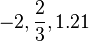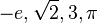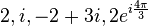MATEMATIKA
Matematika (dari bahasa Yunani: μαθηματικά - mathēmatiká) adalah studi besaran, struktur, ruang, dan perubahan. Para matematikawan mencari berbagai pola, merumuskan konjektur baru, dan membangun kebenaran melalui metode deduksi yang kaku dari aksioma-aksioma dan definisi-definisi yang bersesuaian.
Terdapat perselisihan tentang apakah objek-objek matematika seperti bilangan dan titik hadir secara alami, atau hanyalah buatan manusia. Seorang matematikawanBenjamin Peirce menyebut matematika sebagai "ilmu yang menggambarkan simpulan-simpulan yang penting". Di pihak lain, Albert Einstein menyatakan bahwa "sejauh hukum-hukum matematika merujuk kepada kenyataan, mereka tidaklah pasti; dan sejauh mereka pasti, mereka tidak merujuk kepada kenyataan."
Melalui penggunaan penalaran logika dan abstraksi, matematika berkembang dari pencacahan, perhitungan, pengukuran, dan pengkajian sistematis terhadap bangun danpergerakan benda-benda fisika. Matematika praktis telah menjadi kegiatan manusia sejak adanya rekaman tertulis. Argumentasi kaku pertama muncul di dalam Matematika Yunani, terutama di dalam karya Euklides, Elemen. Matematika selalu berkembang, misalnya di Cina pada tahun 300 SM, di India pada tahun 100 M, dan di Arab pada tahun 800 M, hingga zaman Renaisans, ketika temuan baru matematika berinteraksi dengan penemuan ilmiah baru yang mengarah pada peningkatan yang cepat di dalam laju penemuan matematika yang berlanjut hingga kini.
Kini, matematika digunakan di seluruh dunia sebagai alat penting di berbagai bidang, termasuk ilmu alam, teknik, kedokteran/medis, dan ilmu sosial seperti ekonomi, danpsikologi. Matematika terapan, cabang matematika yang melingkupi penerapan pengetahuan matematika ke bidang-bidang lain, mengilhami dan membuat penggunaan temuan-temuan matematika baru, dan kadang-kadang mengarah pada pengembangan disiplin-disiplin ilmu yang sepenuhnya baru, seperti statistika dan teori permainan. Para matematikawan juga bergulat di dalam matematika murni, atau matematika untuk perkembangan matematika itu sendiri, tanpa adanya penerapan di dalam pikiran, meskipun penerapan praktis yang menjadi latar munculnya matematika murni ternyata seringkali ditemukan terkemudian.
1. Etimologi
Kata "matematika" berasal dari bahasa Yunani Kuno μάθημα (máthēma), yang berarti pengkajian, pembelajaran, ilmu, yang ruang lingkupnya menyempit, dan arti teknisnya menjadi "pengkajian matematika", bahkan demikian juga pada zaman kuno. Kata sifatnya adalah μαθηματικός (mathēmatikós), berkaitan dengan pengkajian, atau tekun belajar, yang lebih jauhnya berarti matematis. Secara khusus, μαθηματικὴ τέχνη (mathēmatikḗ tékhnē), di dalam bahasa Latin ars mathematica, berarti seni matematika.
Bentuk jamak sering dipakai di dalam bahasa Inggris, seperti juga di dalam bahasa Perancis les mathématiques (dan jarang digunakan sebagai turunan bentuk tunggal la mathématique), merujuk pada bentuk jamak bahasa Latin yang cenderung netral mathematica (Cicero), berdasarkan bentuk jamak bahasa Yunani τα μαθηματικά (ta mathēmatiká), yang dipakai Aristotle, yang terjemahan kasarnya berarti "segala hal yang matematis". Tetapi, di dalam bahasa Inggris, kata benda mathematics mengambil bentuk tunggal bila dipakai sebagai kata kerja. Di dalam ragam percakapan, matematika kerap kali disingkat sebagai mathdi Amerika Utara dan maths di tempat lain.
Evolusi matematika dapat dipandang sebagai sederetan abstrak yang selalu bertambah banyak, atau perkataan lainnya perluasan pokok masalah. Abstraksi mula-mula, yang juga berlaku pada banyak binatang, adalah tentang bilangan : pernyataan bahwa dua apel dan dua jeruk (sebagai contoh) memiliki jumlah yang sama.
Selain mengetahui cara mencacah objek-objek fisika, manusia prasejarah juga mengenali cara mencacah besaran abstrak, seperti waktu, hari, musim, tahun. Aritmatika dasar (penjumlahan, pengurangan, perkaliaan dan pembagiaan) mengikuti secara alami.
Langkah selanjutnya memerlukan penulisan atau sistem lain untuk mencatatkan bilangan, semisal tali atau dawai bersimpul yang disebut quipu dipakai oleh bangsa Inca untuk menyimpan data numerik.Sistem bilangan ada banyak dan bermacam-macam, bilangan tertulis yang pertama diketahui ada di dalam naskah warisan Mesir Kuno di Kerajaan Tengah Mesir, Lembah Matematika Rhind.
2. Sejarah
Penggunaan terkuno matematika adalah di dalam perdagangan, pengukuran tanah, pelukisan dan pola-pola penemuan dan pencatatan waktu dan tidak pernah berkembang luas hingga tahun 3000 SM ke muka ketika orang Babilinia dan Mesir Kuno mulai menggunakan Aritmatika, Aljabar dan Geometri untuk penghitungan pajak dan urusan keuangan lainnya, bangunan dan konstruksi, dan Astronomi. Pengkajian matematika yang sistematis di dalam kebenarannya sendiri dimulai pada zaman Yunani Kuno antara tahun 600 dan 300 SM.
Matematika sejak saat itu segera berkembang luas, dan terdapat interaksi bermanfaat antara matematika dan sains , menguntungkan kedua belah pihak. Penemuan-penemuan matematika dibuat sepanjang sejarah dan berlanjut hingga kini. Menurut Mikhail B. Sevryuk, pada Januari 2006 terbitan Bulletin of the American Mathematical Society , "Banyaknya makalah dan buku yang dilibatkan di dalam basis data Mathematical Reviews sejak 1940 (tahun pertama beroperasinya MR) kini melebihi 1,9 juta, dan melebihi 75 ribu artikel ditambahkan ke dalam basis data itu tiap tahun. Sebagian besar karya di samudera ini berisi teorema matematika baru beserta bukti-buktinya.
3. Bidang-bidang Matematika
Disiplin-disiplin utama di dalam matematika pertama muncul karena kebutuhan akan perhitungan di dalam perdagangan, untuk memahami hubungan antarbilangan, untuk mengukur tanah, dan untuk meramal peristiwa astronomi. Empat kebutuhan ini secara kasar dapat dikaitkan dengan pembagian-pembagian kasar matematika ke dalam pengkajian besaran, struktur, ruang, dan perubahan (yakni aritmatika, aljabar, geometri dan analisis). Selain pokok bahasan itu, juga terdapat pembagian-pembagian yang dipersembahkan untuk pranala-pranala penggalian dari jantung matematika ke lapangan-lapangan lain: ke logika , ke teori himpunan (dasar), ke matematika empirik dari aneka macam ilmu pengetahuan (matematika terapan), dan yang lebih baru adalah ke pengkajian kaku akan ketakpastian.
a. Besaran
Pengkajian besaran dimulakan dengan bilanan , pertama bilangan aslli dan bilangan bulat ("semua bilangan") dan operasi aritmetika di ruang bilangan itu, yang dipersifatkan di dalam aritmatika . Sifat-sifat yang lebih dalam dari bilangan bulat dikaji di dalam teori bilangan, dari mana datangnya hasil-hasil popular seperti Teorema Terakhir Fermat . Teori bilangan juga memegang dua masalah tak terpecahkan : konjektur prima kembar dan konjektur goldbach.
Karena sistem bilangan dikembangkan lebih jauh, bilangan bulat diakui sebagai himpunan bagian dari bilangan rasional (pecahan). Sementara bilangan pecahan berada di dalam bioa bilangan real, yang dipakai untuk menyajikan besaran-besaran kontinu. Bilangan real diperumum menjadi bilangan kompleks. Inilah langkah pertama dari jenjang bilangan yang beranjak menyertakan kuarternion dan oktonion. Perhatian terhadap bilangan asli juga mengarah pada bilangan transfinit, yang memformalkan konsep pencacahan ketakhinggan. Wilayah lain pengkajian ini adalah ukuran, yang mengarah pada bilangan kardinal dan kemudian pada konsepsi ketakhinggaan lainnya : bilangan aleph, yang memungkinkan perbandingan bermakna tentang ukuran himpunan-himpunan besar ketakhinggaan.
b. Ruang
Pengkajian ruang bermula dengan geometri – khususnya, geometri euclid . Trigonometri memadukan ruang dan bilangan, dan mencakupi Teorema pitagoras yang terkenal. Pengkajian modern tentang ruang memperumum gagasan-gagasan ini untuk geometri berdimensi lebih tinggi, geometri tak-euclid (yang berperan penting di dalam relativitas umum) dan topologi. Besaran dan ruang berperan penting di dalam geometri analitik, geometri digerensial dan geometri diferensial serta geometri aljabar. Di dalam geometri diferensial terdapat konsep-konsep buntelan serat dan kalkulus lipatan. Di dalam geometri aljabar terdapat penjelasan objek-objek geometri sebagai himpunan penyelesaian persamaan polinom, memadukan konsep-konsep besaran dan ruang, dan juga pengkajian grup topologi, yang memadukan struktur dan ruang. Grup lie biasa dipakai untuk mengkaji ruang, struktur, dan perubahan. Topologi di dalam banyak percabangannya mungkin menjadi wilayah pertumbuhan terbesar di dalam matematika abad ke-20, dan menyertakan konjektur poincare yang telah lama ada dan teorema empat warna, yang hanya "berhasil" dibuktikan dengan komputer, dan belum pernah dibuktikan oleh manusia secara manual.
Memahami dan menjelaskan perubahan adalah tema biasa di dalam ilmu pengetahuan alam, dan kalkulus telah berkembang sebagai alat yang penuh-daya untuk menyeledikinya. Fungsi-fungsi muncul di sini, sebagai konsep penting untuk menjelaskan besaran yang berubah. Pengkajian kaku tentang bilangan real dan fungsi-fungsi berpeubah real dikenal sebagai analisis real, dengan analisis kompleks lapangan yang setara untuk bilangan kompleks. Hipotesis Riemann, salah satu masalah terbuka yang paling mendasar di dalam matematika, dilukiskan dari analisis kompleks. Analisis fungsional memusatkan perhatian pada ruang fungsi (biasanya berdimensi tak-hingga). Satu dari banyak terapan analisis fungsional adalah mekanika kuantum. Banyak masalah secara alami mengarah pada hubungan antara besaran dan laju perubahannya, dan ini dikaji sebagai persamaan diferensial. Banyak gejala di alam dapat dijelaskan menggunakan sistem dinamika; teori kekacauan mempertepat jalan-jalan di mana banyak sistem ini memamerkan perilaku deterministik yang masih saja belum terdugakan.
Banyak objek matematika, semisal himpunan bilangan dan fungsi, memamerkan struktur bagian dalam. Sifat-sifat struktural objek-objek ini diselidiki di dalam pengkajian grup, gelanggang, lapangan dan sistem abstrak lainnya, yang mereka sendiri adalah objek juga. Ini adalah lapangan aljabar abstrak. Sebuah konsep penting di sini yakni vektor, diperumum menjadi ruang vektor, dan dikaji di dalam aljabar linear. Pengkajian vektor memadukan tiga wilayah dasar matematika: besaran, struktur, dan ruang. Kalkulus vektor memperluas lapangan itu ke dalam wilayah dasar keempat, yakni perubahan. Kalkulus tensor mengkajikesetangkupan dan perilaku vektor yang dirotasi. Sejumlah masalah kuno tentang Kompas dan konstruksi garis lurus akhirnya terpecahkan oleh Teori galois.
Untuk memeriksa dasar-dasar matematika, lapangan logika matematika dan teori himpunan dikembangkan, juga teori kategori yang masih dikembangkan. Kata majemuk "krisis dasar" mejelaskan pencarian dasar kaku untuk matematika yang mengambil tempat pada dasawarsa 1900-an sampai 1930-an. Beberapa ketaksetujuan tentang dasar-dasar matematika berlanjut hingga kini. Krisis dasar dipicu oleh sejumlah silang sengketa pada masa itu, termasuk kontroversi teori himpunan Cantor dan kontroversi Brouwer-Hilbert.
Logika matematika diperhatikan dengan meletakkan matematika pada sebuah kerangka kerja aksiomatis yang kaku, dan mengkaji hasil-hasil kerangka kerja itu. Logika matematika adalah rumah bagi Teori ketaklengkapan kedua Gödel, mungkin hasil yang paling dirayakan di dunia logika, yang (secara informal) berakibat bahwa suatu sistem formal yang berisi aritmetika dasar, jika suara (maksudnya semua teorema yang dapat dibuktikan adalah benar), maka tak-lengkap (maksudnya terdapat teorema sejati yang tidak dapat dibuktikan di dalam sistem itu). Gödel menunjukkan cara mengonstruksi, sembarang kumpulan aksioma bilangan teoretis yang diberikan, sebuah pernyataan formal di dalam logika yaitu sebuah bilangan sejati-suatu fakta teoretik, tetapi tidak mengikuti aksioma-aksioma itu. Oleh karena itu, tiada sistem formal yang merupakan aksiomatisasi sejati teori bilangan sepenuhnya. Logika modern dibagi ke dalam teori rekursi, teori model, dan teori pembuktian, dan terpaut dekat dengan ilmu komputer teoretis.
Matematika diskret adalah nama lazim untuk lapangan matematika yang paling berguna di dalam ilmu komputer teoretis. Ini menyertakan teori komputabilitas, teori kompleksitas komputasional, dan teori informasi. Teori komputabilitas memeriksa batasan-batasan berbagai model teoretis komputer, termasuk model yang dikenal paling berdaya - Mesin turing. Teori kompleksitas adalah pengkajian traktabilitas oleh komputer; beberapa masalah, meski secara teoretis terselesaikan oleh komputer, tetapi cukup mahal menurut konteks waktu dan ruang, tidak dapat dikerjakan secara praktis, bahkan dengan cepatnya kemajuan perangkat keras komputer. Pamungkas, teori informasi memusatkan perhatian pada banyaknya data yang dapat disimpan pada media yang diberikan, dan oleh karenanya berkenaan dengan konsep-konsep semisalpemadatan dan entropi.
Sebagai lapangan yang relatif baru, matematika diskret memiliki sejumlah masalah terbuka yang mendasar. Yang paling terkenal adalah masalah "P=NP?", salah satu Masalah Hadiah Milenium.
Matematika terapan berkenaan dengan penggunaan alat matematika abstrak guna memecahkan masalah-masalah konkret di dalam ilmu pengetahuan, bisnis, dan wilayah lainnya. Sebuah lapangan penting di dalam matematika terapan adalah statistika, yang menggunakan teori peluang sebagai alat dan membolehkan penjelasan, analisis, dan peramalan gejala di mana peluang berperan penting. Sebagian besar percobaan, survey, dan pengkajian pengamatan memerlukan statistika. (Tetapi banyak statistikawan, tidak menganggap mereka sendiri sebagai matematikawan, melainkan sebagai kelompok sekutu.) Analisis numerik menyelidiki metode komputasional untuk memecahkan masalah-masalah matematika secara efisien yang biasanya terlalu lebar bagi kapasitas numerik manusia; analisis numerik melibatkan pengkajiangalat pemotongan atau sumber-sumber galat lain di dalam komputasi.
4. Simbol Matematika Dasar
Simbol | Nama | Penjelasan | Contoh |
|---|
| Dibaca sebagai |
|---|
| Kategori |
|---|
= | kesamaan | x = y berarti x and y mewakili hal atau nilai yang sama. | 1 + 1 = 2 |
| sama dengan |
| umum |
≠ | Ketidaksamaan | x ≠ y berarti x dan y tidak mewakili hal atau nilai yang sama. | 1 ≠ 2 |
| tidak sama dengan |
| umum |
<
> | ketidaksamaan | x < y berarti x lebih kecil dari y.
x > y means x lebih besar dari y. | 3 < 4
5 > 4 |
| lebih kecil dari; lebih besar dari |
| order theory |
≤
≥ | inequality | x ≤ y berarti x lebih kecil dari atau sama dengan y.
x ≥ y berarti x lebih besar dari atau sama dengan y. | 3 ≤ 4 and 5 ≤ 5
5 ≥ 4 and 5 ≥ 5 |
| lebih kecil dari atau sama dengan, lebih besar dari atau sama dengan |
| order theory |
+ | tambah | 4 + 6 berarti jumlah antara 4 dan 6. | 2 + 7 = 9 |
| tambah |
| aritmatika |
| disjoint union | A1 + A2 means the disjoint union of sets A1 and A2. | A1={1,2,3,4} ∧ A2={2,4,5,7} ⇒
A1 + A2 = {(1,1), (2,1), (3,1), (4,1), (2,2), (4,2), (5,2), (7,2)} |
| the disjoint union of … and … |
| teori himpunan |
− | kurang | 9 − 4 berarti 9 dikurangi 4. | 8 − 3 = 5 |
| kurang |
| aritmatika |
| tanda negatif | −3 berarti negatif dari angka 3. | −(−5) = 5 |
| negatif |
| aritmatika |
| set-theoretic complement | A − B berarti himpunan yang mempunyai semua anggota dari A yang tidak terdapat pada B. | {1,2,4} − {1,3,4} = {2} |
| minus; without |
| set theory |
× | multiplication | 3 × 4 berarti perkalian 3 oleh 4. | 7 × 8 = 56 |
| kali |
| aritmatika |
| Cartesian product | X×Y means the set of all ordered pairs with the first element of each pair selected from X and the second element selected from Y. | {1,2} × {3,4} = {(1,3),(1,4),(2,3),(2,4)} |
| the Cartesian product of … and …; the direct product of … and … |
| teori himpunan |
| cross product | u × v means the cross product of vectors u and v | (1,2,5) × (3,4,−1) =
(−22, 16, − 2) |
| cross |
| vector algebra |
÷
/ | division | 6 ÷ 3 atau 6/3 berati 6 dibagi 3. | 2 ÷ 4 = .5
12/4 = 3 |
| bagi |
| aritmatika |
√ | square root | √x berarti bilangan positif yang kuadratnya x. | √4 = 2 |
| akar kuadrat |
| bilangan real |
| complex square root | if z = r exp(iφ) is represented in polar coordinates with -π < φ ≤ π, then √z = √r exp(iφ/2). | √(-1) = i |
| the complex square root of; square root |
| Bilangan kompleks |
| | | absolute value | |x| means the distance in the real line (or the complex plane) between x and zero. | |3| = 3, |-5| = |5|
|i| = 1, |3+4i| = 5 |
| nilai mutlak dari |
| numbers |
! | factorial | n! adalah hasil dari 1×2×...×n. | 4! = 1 × 2 × 3 × 4 = 24 |
| faktorial |
| combinatorics |
~ | probability distribution | X ~ D, means the random variable X has the probability distribution D. | X ~ N(0,1), the standard normal distribution |
| has distribution |
| statistika |
⇒
→
⊃ | material implication | A ⇒ B means if A is true then B is also true; if A is false then nothing is said about B.
→ may mean the same as ⇒, or it may have the meaning for functions given below.
⊃ may mean the same as ⇒, or it may have the meaning for superset given below. | x = 2 ⇒ x2 = 4 is true, but x2 = 4 ⇒ x = 2 is in general false (since x could be −2). |
| implies; if .. then |
| propositional logic |
⇔
↔ | material equivalence | A ⇔ B means A is true if B is true and A is false if B is false. | x + 5 = y +2 ⇔ x + 3 = y |
| if and only if; iff |
| propositional logic |
¬
˜ | logical negation | The statement ¬A is true if and only if A is false.
A slash placed through another operator is the same as "¬" placed in front. | ¬(¬A) ⇔ A
x ≠ y ⇔ ¬(x = y) |
| not |
| propositional logic |
∧ | logical conjunction or meet in a lattice | The statement A ∧ B is true if A and B are both true; else it is false. | n < 4 ∧ n >2 ⇔ n = 3 when n is a natural number. |
| and |
| propositional logic, lattice theory |
∨ | logical disjunction or join in a lattice | The statement A ∨ B is true if A or B (or both) are true; if both are false, the statement is false. | n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 when n is a natural number. |
| or |
| propositional logic, lattice theory |
⊕
⊻ | exclusive or | The statement A ⊕ B is true when either A or B, but not both, are true. A ⊻ B means the same. | (¬A) ⊕ A is always true, A ⊕ A is always false. |
| xor |
| propositional logic, Boolean algebra |
∀ | universal quantification | ∀ x: P(x) means P(x) is true for all x. | ∀ n ∈ N: n2 ≥ n. |
| for all; for any; for each |
| predicate logic |
∃ | existential quantification | ∃ x: P(x) means there is at least one x such that P(x) is true. | ∃ n ∈ N: n is even. |
| there exists |
| predicate logic |
∃! | uniqueness quantification | ∃! x: P(x) means there is exactly one x such that P(x) is true. | ∃! n ∈ N: n + 5 = 2n. |
| there exists exactly one |
| predicate logic |
:=
≡
:⇔ | definition | x := y or x ≡ y means x is defined to be another name for y (but note that ≡ can also mean other things, such as congruence).
P :⇔ Q means P is defined to be logically equivalent to Q. | cosh x := (1/2)(exp x + exp (−x))
A XOR B :⇔ (A ∨ B) ∧ ¬(A ∧ B) |
| is defined as |
| everywhere |
{ , } | set brackets | {a,b,c} means the set consisting of a, b, and c. | N = {0,1,2,...} |
| the set of ... |
| teori himpunan |
{ : }
{ | } | set builder notation | {x : P(x)} means the set of all x for which P(x) is true. {x | P(x)} is the same as {x : P(x)}. | {n ∈ N : n2 < 20} = {0,1,2,3,4} |
| the set of ... such that ... |
| teori himpunan |
∅
{} | himpunan kosong | ∅ berarti himpunan yang tidak memiliki elemen. {} juga berarti hal yang sama. | {n ∈ N : 1 < n2 < 4} = ∅ |
| himpunan kosong |
| teori himpunan |
∈
∉ | set membership | a ∈ S means a is an element of the set S; a ∉ S means a is not an element of S. | (1/2)−1 ∈ N
2−1 ∉ N |
| is an element of; is not an element of |
| everywhere, teori himpunan |
⊆
⊂ | subset | A ⊆ B means every element of A is also element of B.
A ⊂ B means A ⊆ B but A ≠ B. | A ∩ B ⊆ A; Q ⊂ R |
| is a subset of |
| teori himpunan |
⊇
⊃ | superset | A ⊇ B means every element of B is also element of A.
A ⊃ B means A ⊇ B but A ≠ B. | A ∪ B ⊇ B; R ⊃ Q |
| is a superset of |
| teori himpunan |
∪ | set-theoretic union | A ∪ B means the set that contains all the elements from A and also all those from B, but no others. | A ⊆ B ⇔ A ∪ B = B |
| the union of ... and ...; union |
| teori himpunan |
∩ | set-theoretic intersection | A ∩ B means the set that contains all those elements that A and B have in common. | {x ∈ R : x2 = 1} ∩ N = {1} |
| intersected with; intersect |
| teori himpunan |
\ | set-theoretic complement | A \ B means the set that contains all those elements of A that are not in B. | {1,2,3,4} \ {3,4,5,6} = {1,2} |
| minus; without |
| teori himpunan |
( ) | function application | f(x) berarti nilai fungsi f pada elemen x. | Jika f(x) := x2, maka f(3) = 32 = 9. |
| of |
| teori himpunan |
| precedence grouping | Perform the operations inside the parentheses first. | (8/4)/2 = 2/2 = 1, but 8/(4/2) = 8/2 = 4. |
|
| umum |
f:X→Y | function arrow | f: X → Y means the function f maps the set X into the set Y. | Let f: Z → N be defined by f(x) = x2. |
| from ... to |
| teori himpunan |
o | function composition | fog is the function, such that (fog)(x) = f(g(x)). | if f(x) = 2x, and g(x) = x + 3, then (fog)(x) = 2(x + 3). |
| composed with |
| teori himpunan |
N
ℕ | Bilangan asli | N berarti {0,1,2,3,...}, but see the article on natural numbers for a different convention. | {|a| : a ∈ Z} = N |
| N |
| Bilangan |
Z
ℤ | Bilangan bulat | Z berarti {...,−3,−2,−1,0,1,2,3,...}. | {a : |a| ∈ N} = Z |
| Z |
| Bilangan |
Q
ℚ | Bilangan rasional | Q berarti {p/q : p,q ∈ Z, q ≠ 0}. | 3.14 ∈ Q
π ∉ Q |
| Q |
| Bilangan |
R
ℝ | Bilangan real | R berarti {limn→∞ an : ∀ n ∈ N: an ∈ Q, the limit exists}. | π ∈ R
√(−1) ∉ R |
| R |
| Bilangan |
C
ℂ | Bilangan kompleks | C means {a + bi : a,b ∈ R}. | i = √(−1) ∈ C |
| C |
| Bilangan |
∞ | infinity | ∞ is an element of the extended number line that is greater than all real numbers; it often occurs in limits. | limx→0 1/|x| = ∞ |
| infinity |
| numbers |
π | pi | π berarti perbandingan (rasio) antara keliling lingkaran dengan diameternya. | A = πr² adalah luas lingkaran dengan jari-jari (radius) r |
| pi |
| Euclidean geometry |
|| || | norm | ||x|| is the norm of the element x of a normed vector space. | ||x+y|| ≤ ||x|| + ||y|| |
| norm of; length of |
| linear algebra |
∑ | summation | ∑k=1n ak means a1 + a2 + ... + an. | ∑k=14 k2 = 12 + 22 + 32 + 42 = 1 + 4 + 9 + 16 = 30 |
| sum over ... from ... to ... of |
| aritmatika |
∏ | product | ∏k=1n ak means a1a2···an. | ∏k=14 (k + 2) = (1 + 2)(2 + 2)(3 + 2)(4 + 2) = 3 × 4 × 5 × 6 = 360 |
| product over ... from ... to ... of |
| aritmatika |
| Cartesian product | ∏i=0nYi means the set of all (n+1)-tuples (y0,...,yn). | ∏n=13R = Rn |
| the Cartesian product of; the direct product of |
| set theory |
' | derivative | f '(x) is the derivative of the function f at the point x, i.e., the slope of the tangent there. | If f(x) = x2, then f '(x) = 2x |
| … prime; derivative of … |
| kalkulus |
∫ | indefinite integral or antiderivative | ∫ f(x) dx means a function whose derivative is f. | ∫x2 dx = x3/3 + C |
| indefinite integral of …; the antiderivative of … |
| kalkulus |
| definite integral | ∫ab f(x) dx means the signed |